Statements (58)
| Predicate | Object |
|---|---|
| gptkbp:instanceOf |
gptkb:mathematical_concept
gptkb:train |
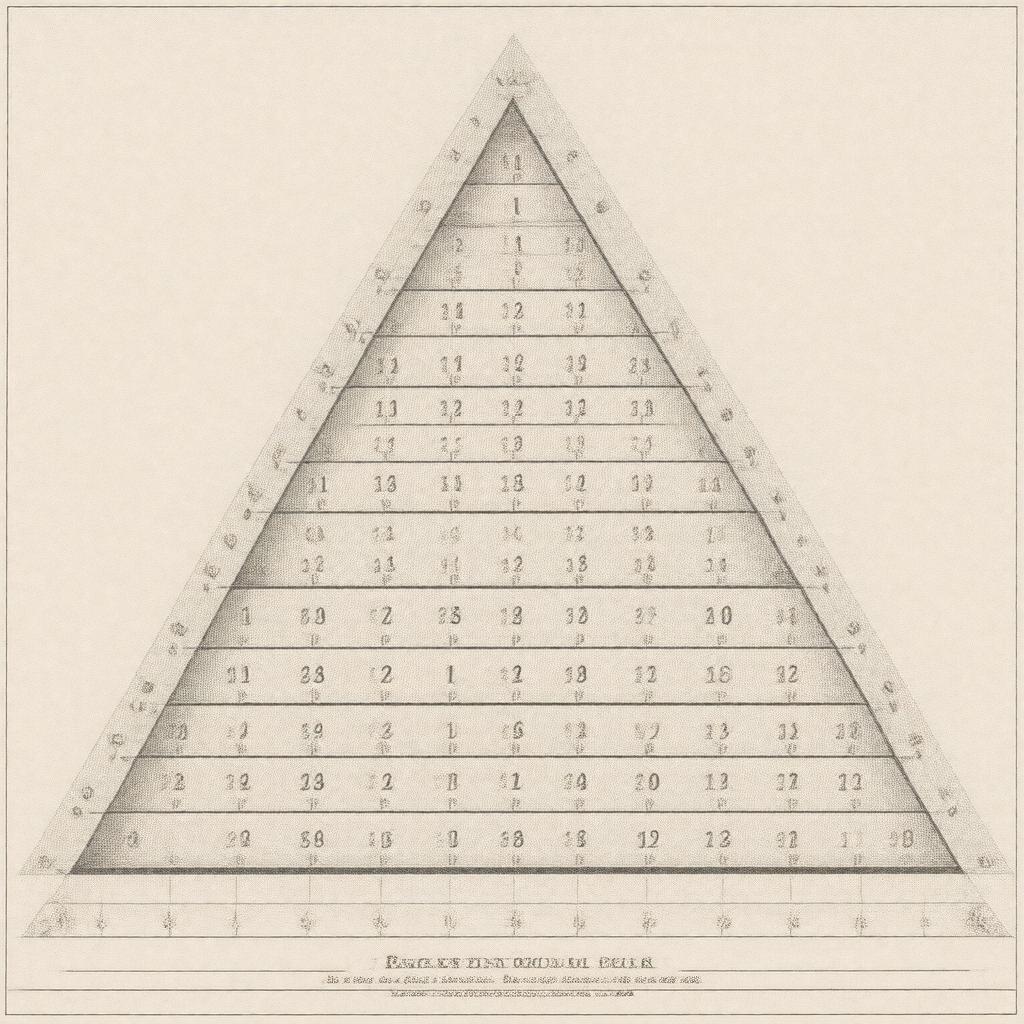
| gptkbp:fifthRow |
1 4 6 4 1
|
| gptkbp:firstRow |
1
|
| gptkbp:fourthRow |
1 3 3 1
|
| https://www.w3.org/2000/01/rdf-schema#label |
Pascal's triangle
|
| gptkbp:namedAfter |
gptkb:Blaise_Pascal
|
| gptkbp:property |
infinite
symmetric appears in Lucas' theorem appears in Pascal's identity appears in Pascal's rule appears in algebra appears in algebraic identities appears in binomial expansions appears in binomial identities appears in binomial theorem appears in calculus appears in combinatorial identities appears in combinatorial proofs appears in combinatorics appears in discrete mathematics appears in fractal geometry appears in hockey stick identity appears in mathematical education appears in mathematical induction appears in mathematical patterns appears in mathematical puzzles appears in multinomial coefficients appears in number theory appears in polynomial expansions appears in polynomial interpolation appears in probability calculations appears in probability distributions appears in probability mass functions appears in probability theory appears in recreational mathematics appears in recursive relations appears in sequence analysis contains Catalan numbers contains Sierpinski triangle pattern modulo 2 contains powers of 2 as row sums contains tetrahedral numbers contains triangular numbers diagonals sum to Fibonacci numbers left and right edges are all 1 rows correspond to powers of 11 up to row 4 each number is the sum of the two numbers directly above it |
| gptkbp:rowN |
contains the coefficients of (a+b)^n
|
| gptkbp:secondRow |
1 1
|
| gptkbp:thirdRow |
1 2 1
|
| gptkbp:usedFor |
gptkb:algebra
gptkb:probability_theory binomial coefficients combinatorics number patterns |
| gptkbp:bfsParent |
gptkb:binomial_theorem
|
| gptkbp:bfsLayer |
5
|